Dagger2 is hard, but it can be easy, part 5
In the previous post we’ve explored scope operators.
In this post we’ll encounter subcomponents and their hierarchy, custom scopes and let’s not waste any time.
Starting off by including the androidx.preferences library
1
implementation 'androidx.preference:preference-ktx:1.1.1'
Let’s delete all the classes from previous posts and remove all of the code within MainActivity also rename TestApplication to
1
2
3
4
5
6
class DaggerIsEasyApplication : Application() {
override fun onCreate() {
super.onCreate()
}
}
Create a simple shared preference manager that’ll hide most of the logic
1
2
3
4
5
6
7
8
9
10
11
12
13
14
@Singleton
class SharedPreferencesManager @Inject constructor(context: Context) {
private companion object {
private const val FIRST_TIME_LAUNCH_KEY = "firstTimeLaunch"
}
private val sharedPrefs = PreferenceManager.getDefaultSharedPreferences(context)
val firstTimeLaunchSinceInstall get() = sharedPrefs.getBoolean(FIRST_TIME_LAUNCH_KEY, true)
fun appHasBeenLaunchedForTheFirstTime() = sharedPrefs.edit(true) {
putBoolean(FIRST_TIME_LAUNCH_KEY, false)
}
}
Annotate it with the scope @Singleton because this instance needs to be alive for the app’s lifetime since that’s when we’ll create the graph.
The second thing we do is create our component and we do the following
1
2
3
4
5
@Component
@Singleton
interface SingletonComponent {
fun provideGraphInside(application: DaggerIsEasyApplication)
}
we press build or F10 and then we go in our Application inheritance to do the following
1
2
3
4
5
6
7
8
class DaggerIsEasyApplication : Application() {
override fun onCreate() {
DaggerSingletonComponent.create().provideGraphInside(this)
super.onCreate()
}
}
Now we get to the real deal, we need an instance of our PreferenceManager inside the application level, then we have something like.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class DaggerIsEasyApplication : Application() {
@Inject
lateinit var sharedPreferencesManager: SharedPreferencesManager
override fun onCreate() {
DaggerSingletonComponent.create().provideGraphInside(this)
super.onCreate()
if (sharedPreferencesManager.firstTimeLaunchSinceInstall){
Log.d(this::class.java.simpleName, "App is launched for the first time since installation time")
sharedPreferencesManager.appHasBeenLaunchedForTheFirstTime()
}
}
}
If we click compile, this will go ahead and compile but there’s one big issue, when we run the app we get something like
1
2
error: [Dagger/MissingBinding] android.content.Context cannot be provided without an @Provides-annotated method.
public abstract interface SingletonComponent
that’s because we need a Context in our SharedPreferencesManager, let’s to do the following changes in our SingletonComponent
1
2
3
4
5
6
7
8
9
10
@Component
@Singleton
interface SingletonComponent {
@Component.Factory
interface SingletonComponentFactory {
fun create(@BindsInstance context: Context): SingletonComponent
}
fun provideGraphInside(application: DaggerIsEasyApplication)
}
We’ve learnt about a new citizen in the Dagger world @Component.Factory a factory has to create our component, because our component needs a parameter in this case a Context, in order to create our SharedPreferencesManager, because Dagger doesn’t know how to get a Context we have to provide it to Dagger ourselves.
Inside we have an interface which is essentially our factory and one important function called create, which returns (creates) the SingletonComponent but with a parameter of the type we wanted, in our case a Context.
Also there’s @BindsInstance, this annotation knows about the type of the parameter in our case Context and later on whenever we request this Context within our @Singleton scope we’ll have it provided to us by Dagger we don’t have to do anything else (because this runtime variable is tied to the component’s scope that binds it, in our case SingletonComponent and it’s children, more about that later on).
As I mentioned earlier, Dagger would be far easier without Android’s runtime, but Context is a runtime variable which is available once the app’s started and that’s what complicates things.
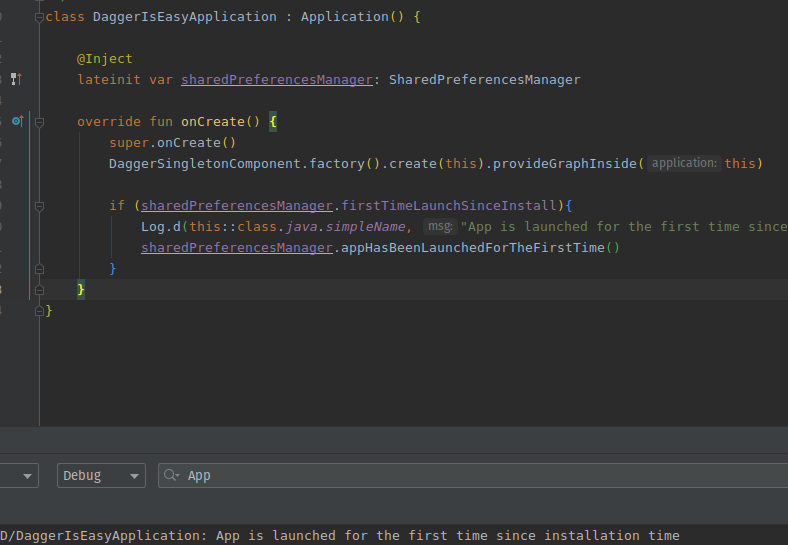
Now for the most important part, let’s create the component with a runtime variable, inside DaggerIsEasyApplication and after onCreate() just right before the super call
1
2
3
4
5
6
7
8
9
override fun onCreate() {
DaggerSingletonComponent.factory().create(this).provideGraphInside(this)
super.onCreate()
if (sharedPreferencesManager.firstTimeLaunchSinceInstall){
Log.d(this::class.java.simpleName, "App is launched for the first time since installation time")
sharedPreferencesManager.appHasBeenLaunchedForTheFirstTime()
}
}
now when we launch the application, we see the following log
when we rerun the app, we won’t see the log.
Let’s say we wanted to get that same SharedPreferencesManager in our MainActivity
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class MainActivity : AppCompatActivity() {
@Inject
lateinit var sharedPreferencesManager: SharedPreferencesManager
override fun onCreate(savedInstanceState: Bundle?) {
super.onCreate(savedInstanceState)
setContentView(R.layout.activity_main)
if (sharedPreferencesManager.firstTimeLaunchMainActivitySinceInstall){
Log.d(this::class.java.simpleName, "Main activity is launched for the first time since installation time")
sharedPreferencesManager.mainActivityHasBeenLaunchedForTheFirstTime()
}
}
}
run the code and see it crash 💥
1
Caused by: kotlin.UninitializedPropertyAccessException: lateinit property sharedPreferencesManager has not been initialized
The first thing that we need to do is make our ApplicationComponent available to do more than one thing, so we expose it as a variable that we initialize with our create(this) and we also provideGraphInside the application level.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class DaggerIsEasyApplication : Application() {
lateinit var applicationComponent: SingletonComponent
private set
@Inject
lateinit var sharedPreferencesManager: SharedPreferencesManager
override fun onCreate() {
super.onCreate()
applicationComponent = DaggerSingletonComponent.factory().create(this).also { it.provideGraphInside(this) }
if (sharedPreferencesManager.firstTimeLaunchSinceInstall) {
Log.d(this::class.java.simpleName, "App is launched for the first time since installation time")
sharedPreferencesManager.appHasBeenLaunchedForTheFirstTime()
}
}
}
Now SingletonComponent is @Singleton scoped, that means we’ve gotta come with our own scoping if we need something inside an Activity.
1
2
3
4
@Scope
@MustBeDocumented
@Retention(AnnotationRetention.RUNTIME)
annotation class ActivityScoped
as we know that we need an Activity component as well, we create one too, now this time we annotate it with @Subcomponent and annotate it with our own scope ActivityScoped. Since this is a subcomponent we need a @Subcomponent.Factory just like we did with the singleton component (there it was a Component.Factory).
1
2
3
4
5
6
7
8
9
10
11
@Subcomponent
@ActivityScoped
interface ActivityComponent {
@Subcomponent.Factory
interface Factory {
fun create(): ActivityComponent
}
fun inject(mainActivity: MainActivity)
}
The main idea here is that the SingletonComponent is the parent and ActivityComponent is it’s child.
We have to make sure of that, now inside our SingletonComponent we provide the factory that creates ActivityComponent.
ActivityComponent is a child, that means every module we include in the SingletonComponent and instance annotated with @BindsInstance would be available inside the ActivityComponent as well, since it’s like ActivityComponent inherited the public variables from SingletonComponent that were annotated with @BindsInstance.
1
2
3
4
5
6
7
8
9
10
@Component
@Singleton
interface SingletonComponent {
@Component.Factory
interface SingletonComponentFactory {
fun create(@BindsInstance context: Context): SingletonComponent
}
fun activityComponentFactory() : ActivityComponent.Factory
fun provideGraphInside(application: DaggerIsEasyApplication)
}
the last thing we do is call the creation, that happens inside our MainActivity right before onCreate(), just like in our Application.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class MainActivity : AppCompatActivity() {
@Inject
lateinit var sharedPreferencesManager: SharedPreferencesManager
override fun onCreate(savedInstanceState: Bundle?) {
(application as DaggerIsEasyApplication).applicationComponent.activityComponentFactory().create().also {
it.inject(this)
}
super.onCreate(savedInstanceState)
setContentView(R.layout.activity_main)
if (sharedPreferencesManager.firstTimeLaunchMainActivitySinceInstall){
Log.d(this::class.java.simpleName, "Main activity is launched for the first time since installation time")
sharedPreferencesManager.mainActivityHasBeenLaunchedForTheFirstTime()
}
}
}
When we run the app we can see that we’re suffering from success.
For demonstrational purposes, we want to have savedInstanceState: Bundle? as a runtime variable and the intent within the ActivityScoped instances, change the ActivityComponent's subcomponent factory
1
2
3
4
5
@Subcomponent.Factory
interface Factory {
fun create(@BindsInstance savedInstanceState: Bundle?,
@BindsInstance intent: Intent): ActivityComponent
}
and
1
2
override fun onCreate(savedInstanceState: Bundle?) {
(application as DaggerIsEasyApplication).applicationComponent.activityComponentFactory().create(savedInstanceState, intent).also {it.inject(this)}
Let’s pretend that we have a class IntentHandler coming from a library that we didn’t create, and we included it as an implementation, that class receives an Intent param.
1
2
3
4
5
6
7
8
9
10
11
class IntentHandler(private val intent: Intent) {
fun getObfuscatedClipData() = obfuscate(intent.clipData)
private fun obfuscate(clipData: ClipData?): ClipData? {
//some magic obfuscation
//call it magic
//call it true
return clipData
}
}
since we don’t own that class, we have to create a module and make Dagger be aware of it.
1
2
3
4
5
6
@Module
object ActivityModule {
@Provides
@ActivityScoped
fun intentHandler(intent: Intent) = IntentHandler(intent)
}
we use @Provides since the code is coming from outside of our own project, otherwise we could’ve just annotated the class with @ActivityScoped and @Inject constructor() and voila.
However can do the following for example:
1
2
3
4
5
6
7
@ActivityScoped
class Bundler @Inject constructor(private val savedInstanceState: Bundle?) {
fun unbundle(){
savedInstanceState // > perform some magic
}
}
we’ve already provided the runtime argument of savedInstanceState: Bundle? using @BindsInstance, now we can play with it.
Our activity looks like:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class MainActivity : AppCompatActivity() {
@Inject
lateinit var sharedPreferencesManager: SharedPreferencesManager
@Inject
lateinit var intentHandler: IntentHandler
@Inject
lateinit var bundler: Bundler
override fun onCreate(savedInstanceState: Bundle?) {
(application as DaggerIsEasyApplication).applicationComponent.activityComponentFactory().create(
savedInstanceState, intent
).also {it.inject(this)}
super.onCreate(savedInstanceState)
setContentView(R.layout.activity_main)
if (sharedPreferencesManager.firstTimeLaunchMainActivitySinceInstall){
Log.d(this::class.java.simpleName, "Main activity is launched for the first time since installation time")
sharedPreferencesManager.mainActivityHasBeenLaunchedForTheFirstTime()
}
if (intentHandler.getObfuscatedClipData() != null){
Log.d(this::class.java.simpleName, "send obfuscated clip data to server")
} else {
Log.d(this::class.java.simpleName, "obfuscated data not available, ignore")
}
bundler.unbundle()
}
}
Let’s tidy up the tings a little bit, create a file called DaggerExtensions and inside
1
2
3
inline fun AppCompatActivity.injector(action: SingletonComponent.() -> Unit) {
(application as DaggerIsEasyApplication).applicationComponent.action()
}
let’s enjoy a bit tidier code, even tidier when we’ll start using Hilt in the future articles.
Some might argue that you’ll replace vanilla Dagger completely, well… not quite, inside feature modules you’ll still need to know the concepts (especially factories and components) of pure Dagger, because Hilt doesn’t entirely replace Dagger, it’s built on top of Dagger to abstract away the Android’s runtime boilerplate setup that you have to do every time you create a new project.